数学中有哪些漂亮的无字证明?
一幅图胜过千言万语 1.证明 1/2+1/4+1/8+1/16+1/32+1/64+…=1 2.sinθ^2+cosθ^2=1 的几何证明,图中是一个四分之一的单位圆 3. tanθ^2+1=secθ^2 的几何证明 4.cotθ^2+1=cscθ^2 5.两角之和的正弦 sin(x+y)和余弦 cos(x+y)的几何证明 6.两角之差的正弦 sin(x-y)和余弦 cos(x-y)的几何证明 7.单位圆中的正弦 sin(x+y)和余弦 cos(x+y)的几何证明 8.正弦二倍角公式 sin2θ=2sinθcosθ的几何证明 9.余弦二倍角公式 cos2θ=2cosθ-1 的几何证明 10.正切半倍角 tan(θ/2)的几何证明 11.余弦半倍角 cos(θ/2)的几何证明 12.AsinX+BcosX 等式的几何证明 13.两角之和正切 tan(X+Y)的几何证明 14.两角之差正切 tan(X-Y)的几何证明 15.斐波那契数列的恒等式 可谓家喻户晓的斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21 ……这个数列从第三项开始,每一项都等于前两项之和,即 F n+1 = F n + F n-1。 它的通项公式是 有趣的是,这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。 而且当 n 无穷大时, F n-1 / F n 越来越逼近黄金分割数 0.618。正因为它的种种神奇性质,美国数学会甚至从 1960 年代起出版了《斐波纳契数列》季刊。关于斐波那契数列,有一个恒等式是这样的。 这个等式很漂亮,不需要借助复杂的数学推导,它有一个很直观的证明方法。 16. 勾股定理 这个大家小学就学过的古老定理,有着无数传奇故事。我可以很随意的写出她的 10 个不同的证明方法。而路明思(Elisha Scott Loomis)在 《毕达哥拉斯命题》( Pythagorean Proposition)提到这个定理的证明方式居然有 367 种之多,实在让人惊讶。这里给出一个不需要语言的证明方法。 实际上勾股定理是余弦定理的一种特殊情况,而余弦定理的证明,同样可以不用语言。 17. 关于反正切的恒等式 关于反正切,有如下两个很精彩的等式: arctan1/2+arctan1/3=π/4 acrtan1+arctan2+arctan3=π 它们的证明方法也同样精彩。 18. 几何平均值小于算术平均值 这是不等式中最重要和基础的等式: 它也可以通过图形来证明。 注意到△ABC∽△DBA ,可以很轻松地得到AB=√ab。剩下的就显而易见了。 19. 这是奇数的求和公式,下图是当 n=8 时的情形 20. 平方数的求和公式 一个很漂亮的公式,证明的过程令人眼前一亮。 21. 立方数的求和公式 立方数的求和证明与平方数的求和证明方法有些相像: 22.结果为 1/3 的一组分子式 下面是一组分子式,他们的结果都等于 1/3 : 让我们用若干个小球看待这个公式。 23.最受数学家喜爱的无字证明 1989 年的《美国数学月刊》(American Mathematical Monthly)上有一个貌似非常困难的数学问题:下图是由一个个小三角形组成的正六边形棋盘,现在请你用右边的三种(仅朝向不同的)菱形把整个棋盘全部摆满(图中只摆了其中一部分),证明当你摆满整个棋盘后,你所使用的每种菱形数量一定相同。 《美国数学月刊》提供了一个非常帅的“证明”。把每种菱形涂上一种颜色,整个图形瞬间有了立体感,看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面,它们的数目显然应该相等。 它把一个纯组合数学问题和立体空间图形结合在了一起,实在让人拍案叫绝。这个问题及其鬼斧神工般的“证明”流传甚广,深受数学家们的喜爱。死理性派曾经讨论过 这个问题 。同时它还是死理性派 logo 的出处。 24.棋盘上的数学证明 在一个8×8的国际象棋棋盘上,我们可以用32张多米诺骨牌(是两个相连正方形的长方形牌)覆盖整个棋盘上的64个方格。如果将对角线上的两个方格切掉,剩下来的62个格子还能用31张骨牌覆盖住吗? 答案是不能的。每一张骨牌在棋盘上必是覆盖住两个相邻方格,一白一黑。所以 31 张骨牌应该可以盖住 31 个黑格和 31 个白格。而这被切了角的棋盘上的方格有 32 个是一种颜色,另一种颜色是 30 个,因此是不能被 31 张骨牌覆盖的。 但是如果我们切掉的不是颜色相同的两个呢?假如我们从棋盘的任何部位切掉两个颜色不同的方格,那么剩下来的 62 格是否一定能被 31 张骨牌完全盖住?我可以告诉你这是一定能做到的,并且关于这个结论,存在一个非常漂亮的证明。建议读者在继续往下阅读前,可以先自行思考如何证明这个结论。 上图就是那个漂亮的证明。不妨对它再赘述两句。粗黑线条将整个棋盘转变为一条首尾相连、黑白格相间的封闭路线。从这棋盘上切掉任何两个颜色不同的方格,会让这个封闭线路变成两段线路(如果切掉的方格是相连的,那就是一条线路)。在这两段(或一段)线路中,两种颜色的格子数量都是偶数,故分别都可以被若干张骨牌覆盖。从而证明整个棋盘可以被 31 张骨牌完全覆盖。 这个著名的棋盘问题是数学游戏大师马丁•加德纳提出的,而上述精妙绝伦的证明则是数学家哥莫瑞(Ralph Gomory)找到的。它们后来被收录在《意料之外的绞刑和其他数学娱乐》这本书里。 25.自然数求和公式 26.自然数阶梯求和与平方和的关系 27.算术平均数——几何平均数之间的不等式 28.调和平均数——几何平均数——算术平均数——平方平均数之间的不等式 29.算术 - 对数 - 几何平均值不等式 30.单调数列的切比雪夫不等式 31.用注水实验法验证勾股定理 1. 取直角三角形的三边长 a,b,c ,其中 c 为斜边,分别制作成底面边长为 a,b,c 的正方形,高度相等的长方体容器; 2. 将底面边长为 a,b 的正方体容器注满水,再将两个容器中的水倒入底面边长为 c 的容器中; 3. 奇迹发生了,两个容器中的水恰好可以注满第三个容器! 查看知乎讨论

一幅图胜过千言万语
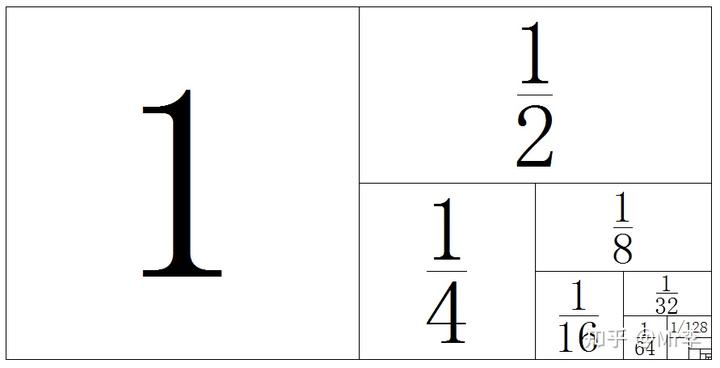
1.证明 1/2+1/4+1/8+1/16+1/32+1/64+…=1
2.sinθ^2+cosθ^2=1 的几何证明,图中是一个四分之一的单位圆
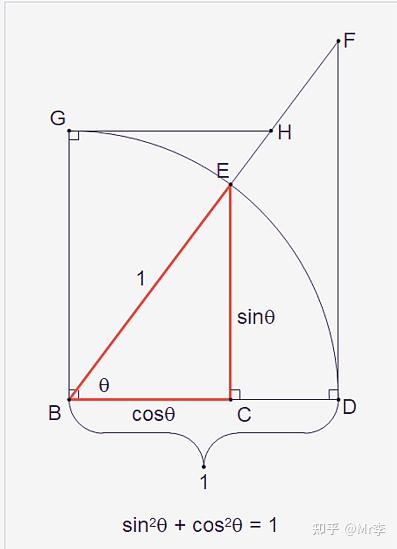
3. tanθ^2+1=secθ^2 的几何证明
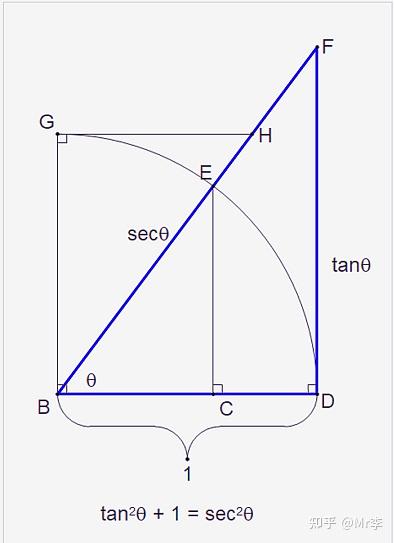
4.cotθ^2+1=cscθ^2
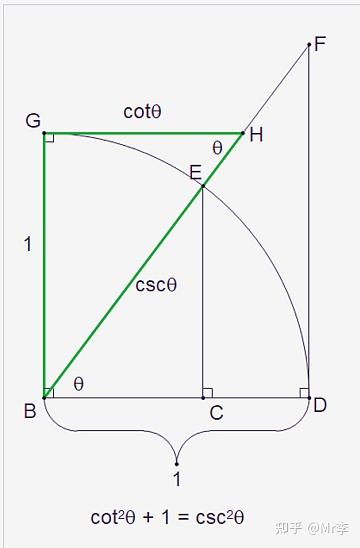
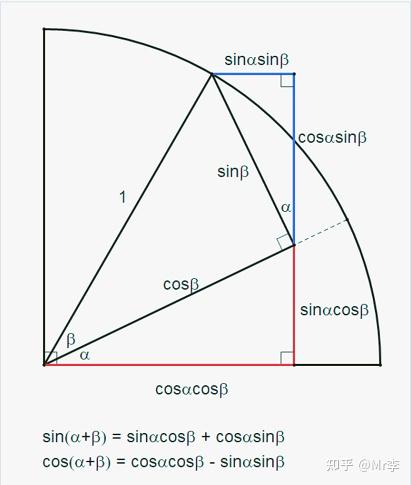
5.两角之和的正弦 sin(x+y)和余弦 cos(x+y)的几何证明
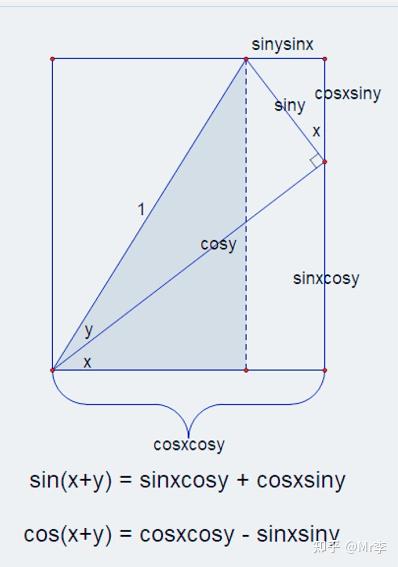
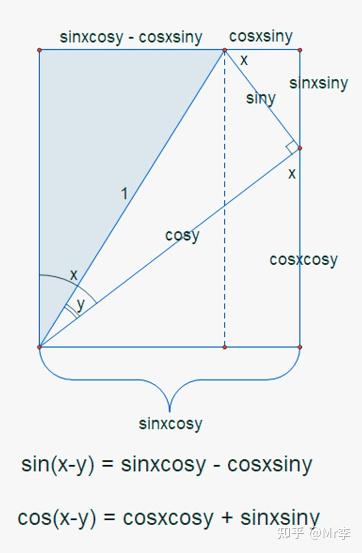
6.两角之差的正弦 sin(x-y)和余弦 cos(x-y)的几何证明
7.单位圆中的正弦 sin(x+y)和余弦 cos(x+y)的几何证明
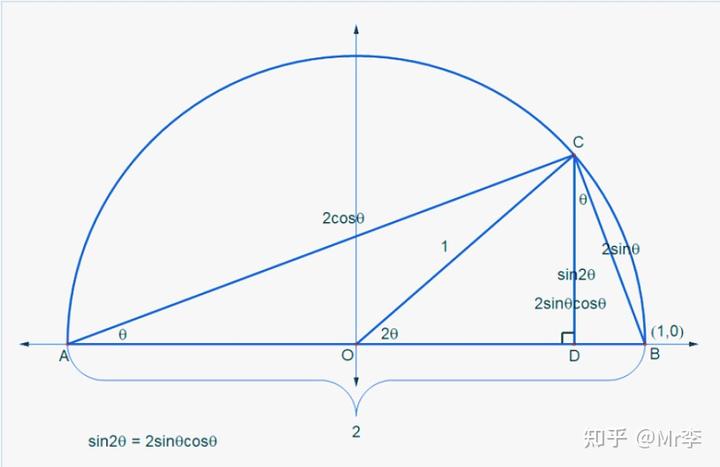
8.正弦二倍角公式 sin2θ=2sinθcosθ的几何证明
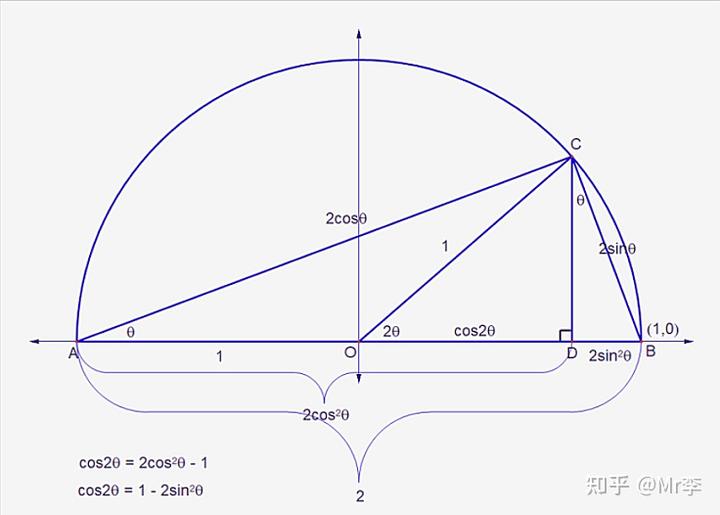
9.余弦二倍角公式 cos2θ=2cosθ-1 的几何证明
10.正切半倍角 tan(θ/2)的几何证明
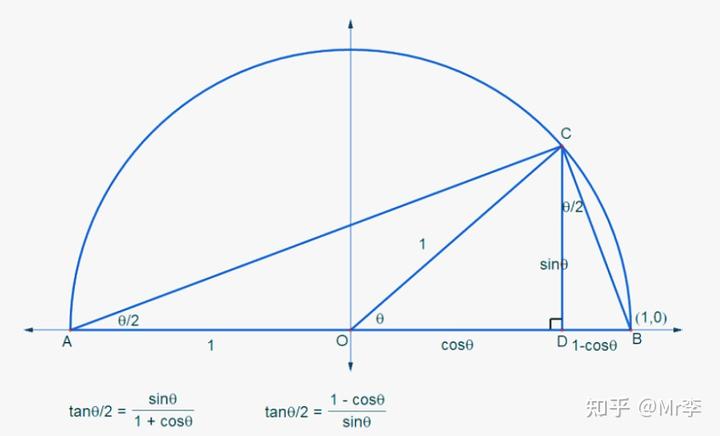
11.余弦半倍角 cos(θ/2)的几何证明
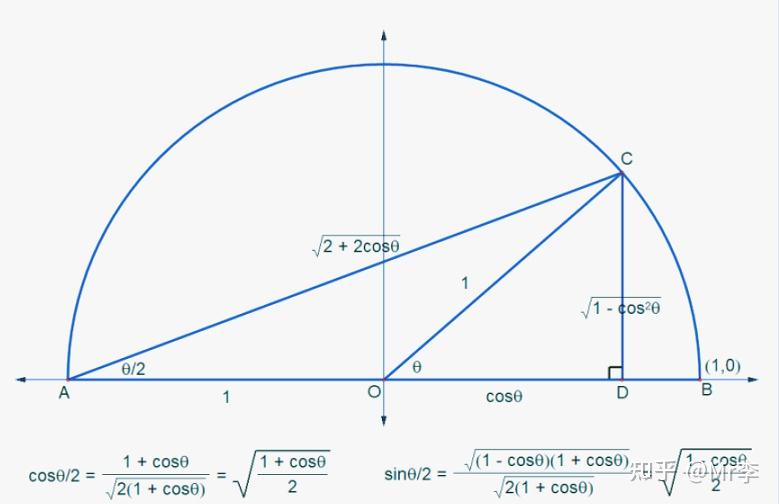
12.AsinX+BcosX 等式的几何证明
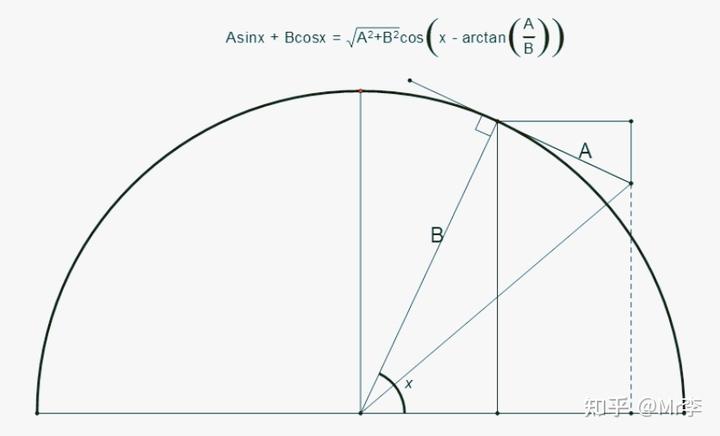
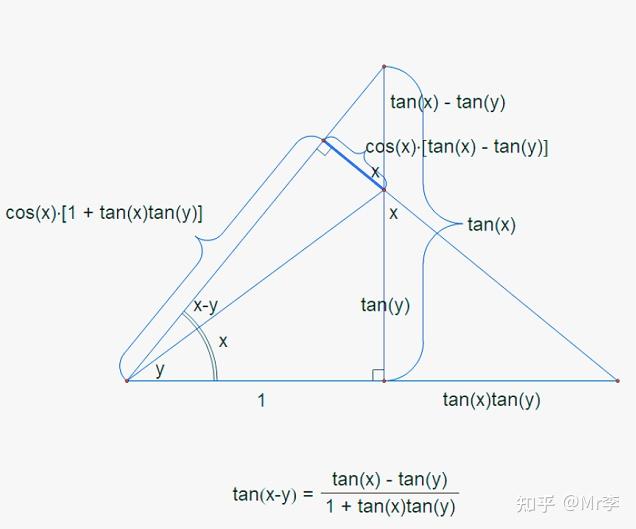
13.两角之和正切 tan(X+Y)的几何证明
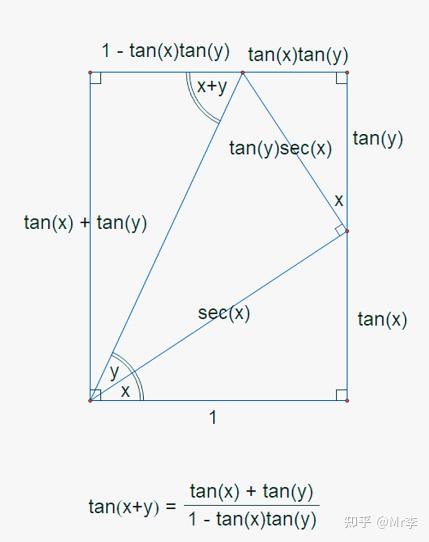
14.两角之差正切 tan(X-Y)的几何证明
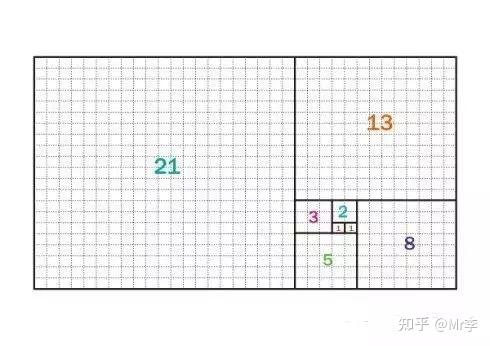
15.斐波那契数列的恒等式
可谓家喻户晓的斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21 ……这个数列从第三项开始,每一项都等于前两项之和,即 F n+1 = F n + F n-1。
它的通项公式是
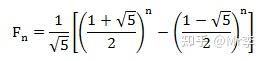
有趣的是,这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。
而且当 n 无穷大时, F n-1 / F n 越来越逼近黄金分割数 0.618。正因为它的种种神奇性质,美国数学会甚至从 1960 年代起出版了《斐波纳契数列》季刊。关于斐波那契数列,有一个恒等式是这样的。
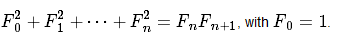
这个等式很漂亮,不需要借助复杂的数学推导,它有一个很直观的证明方法。
16. 勾股定理
这个大家小学就学过的古老定理,有着无数传奇故事。我可以很随意的写出她的 10 个不同的证明方法。而路明思(Elisha Scott Loomis)在 《毕达哥拉斯命题》( Pythagorean Proposition)提到这个定理的证明方式居然有 367 种之多,实在让人惊讶。这里给出一个不需要语言的证明方法。

实际上勾股定理是余弦定理的一种特殊情况,而余弦定理的证明,同样可以不用语言。
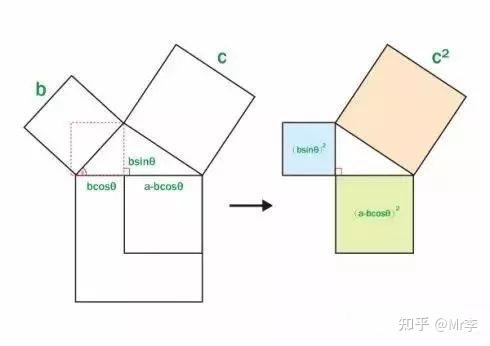
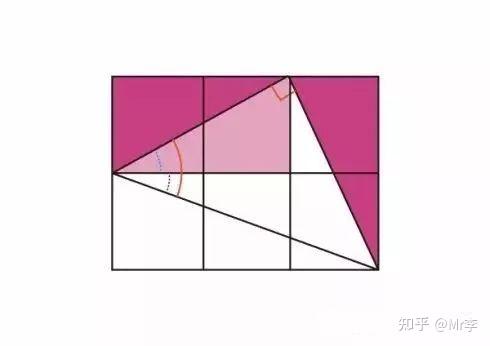
17. 关于反正切的恒等式
关于反正切,有如下两个很精彩的等式:
arctan1/2+arctan1/3=π/4
acrtan1+arctan2+arctan3=π
它们的证明方法也同样精彩。

18. 几何平均值小于算术平均值
这是不等式中最重要和基础的等式:
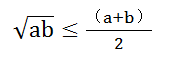
它也可以通过图形来证明。
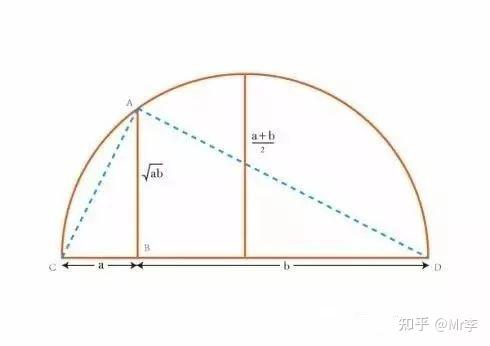
注意到△ABC∽△DBA ,可以很轻松地得到AB=√ab。剩下的就显而易见了。
19.
这是奇数的求和公式,下图是当 n=8 时的情形

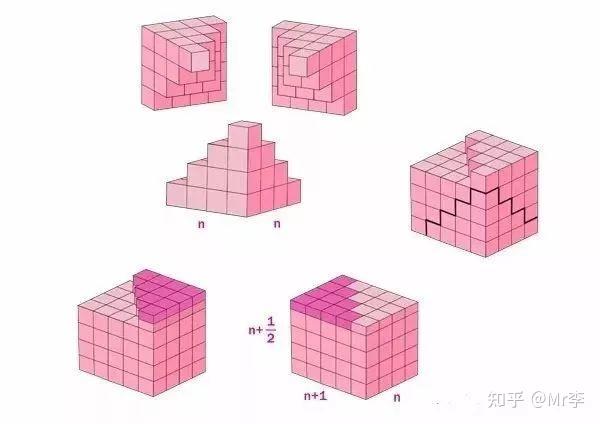
20. 平方数的求和公式
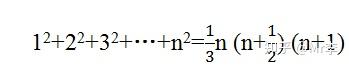
一个很漂亮的公式,证明的过程令人眼前一亮。
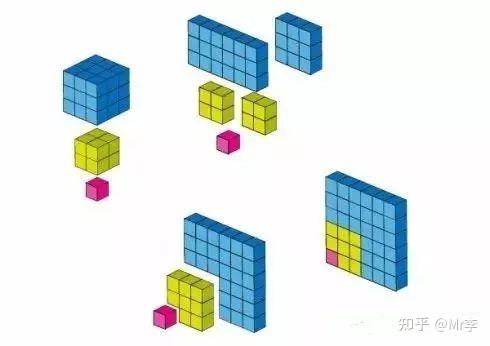
21. 立方数的求和公式
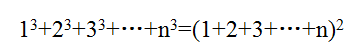
立方数的求和证明与平方数的求和证明方法有些相像:
22.结果为 1/3 的一组分子式
下面是一组分子式,他们的结果都等于 1/3 :
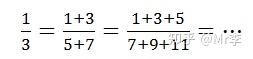
让我们用若干个小球看待这个公式。
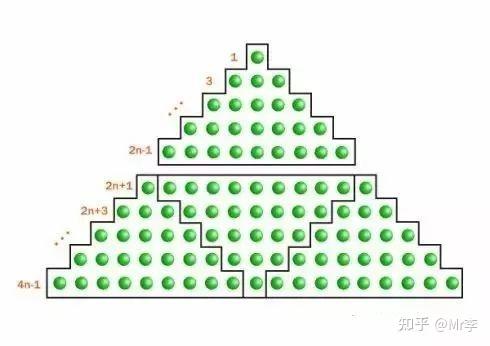
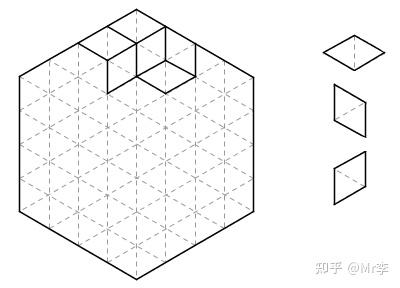
23.最受数学家喜爱的无字证明
1989 年的《美国数学月刊》(American Mathematical Monthly)上有一个貌似非常困难的数学问题:下图是由一个个小三角形组成的正六边形棋盘,现在请你用右边的三种(仅朝向不同的)菱形把整个棋盘全部摆满(图中只摆了其中一部分),证明当你摆满整个棋盘后,你所使用的每种菱形数量一定相同。
《美国数学月刊》提供了一个非常帅的“证明”。把每种菱形涂上一种颜色,整个图形瞬间有了立体感,看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面,它们的数目显然应该相等。
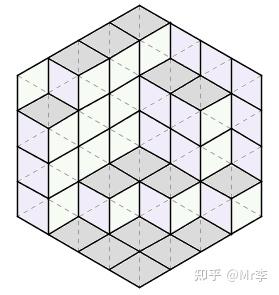
它把一个纯组合数学问题和立体空间图形结合在了一起,实在让人拍案叫绝。这个问题及其鬼斧神工般的“证明”流传甚广,深受数学家们的喜爱。死理性派曾经讨论过 这个问题 。同时它还是死理性派 logo 的出处。
24.棋盘上的数学证明
在一个8×8的国际象棋棋盘上,我们可以用32张多米诺骨牌(是两个相连正方形的长方形牌)覆盖整个棋盘上的64个方格。如果将对角线上的两个方格切掉,剩下来的62个格子还能用31张骨牌覆盖住吗?

答案是不能的。每一张骨牌在棋盘上必是覆盖住两个相邻方格,一白一黑。所以 31 张骨牌应该可以盖住 31 个黑格和 31 个白格。而这被切了角的棋盘上的方格有 32 个是一种颜色,另一种颜色是 30 个,因此是不能被 31 张骨牌覆盖的。
但是如果我们切掉的不是颜色相同的两个呢?假如我们从棋盘的任何部位切掉两个颜色不同的方格,那么剩下来的 62 格是否一定能被 31 张骨牌完全盖住?我可以告诉你这是一定能做到的,并且关于这个结论,存在一个非常漂亮的证明。建议读者在继续往下阅读前,可以先自行思考如何证明这个结论。
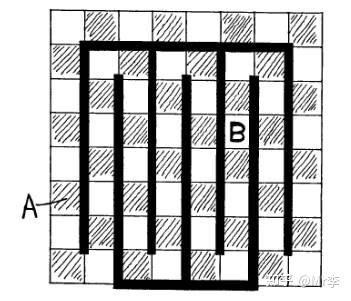
上图就是那个漂亮的证明。不妨对它再赘述两句。粗黑线条将整个棋盘转变为一条首尾相连、黑白格相间的封闭路线。从这棋盘上切掉任何两个颜色不同的方格,会让这个封闭线路变成两段线路(如果切掉的方格是相连的,那就是一条线路)。在这两段(或一段)线路中,两种颜色的格子数量都是偶数,故分别都可以被若干张骨牌覆盖。从而证明整个棋盘可以被 31 张骨牌完全覆盖。
这个著名的棋盘问题是数学游戏大师马丁•加德纳提出的,而上述精妙绝伦的证明则是数学家哥莫瑞(Ralph Gomory)找到的。它们后来被收录在《意料之外的绞刑和其他数学娱乐》这本书里。
25.自然数求和公式
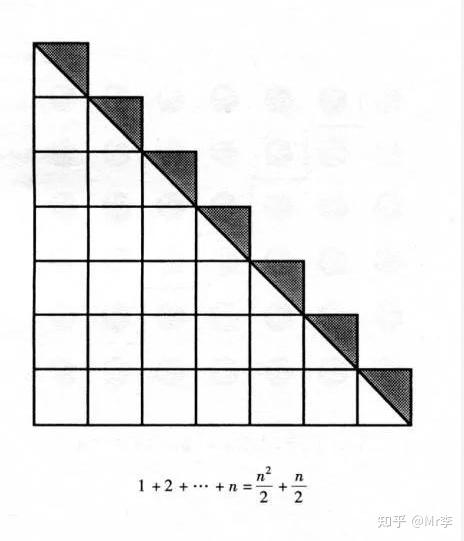
26.自然数阶梯求和与平方和的关系

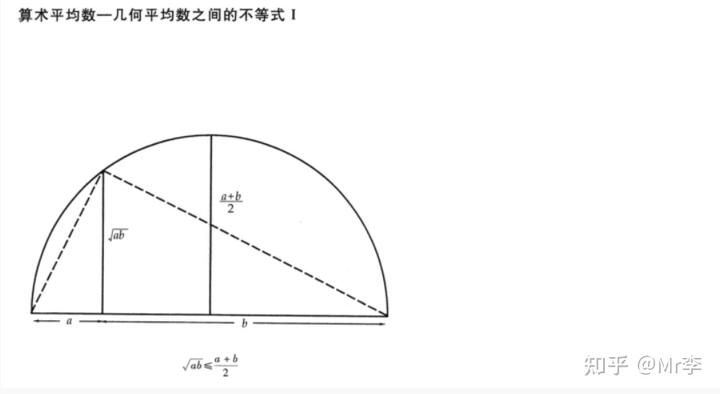
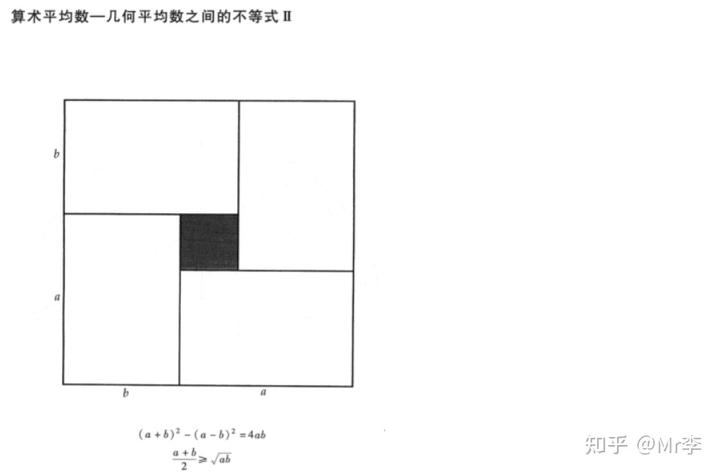
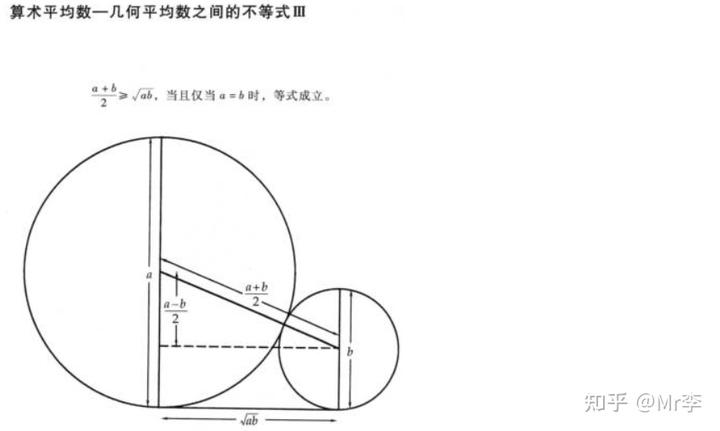
27.算术平均数——几何平均数之间的不等式
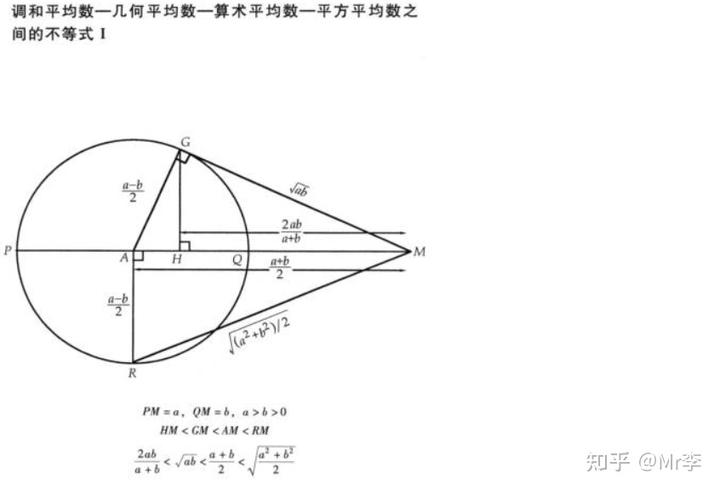
28.调和平均数——几何平均数——算术平均数——平方平均数之间的不等式
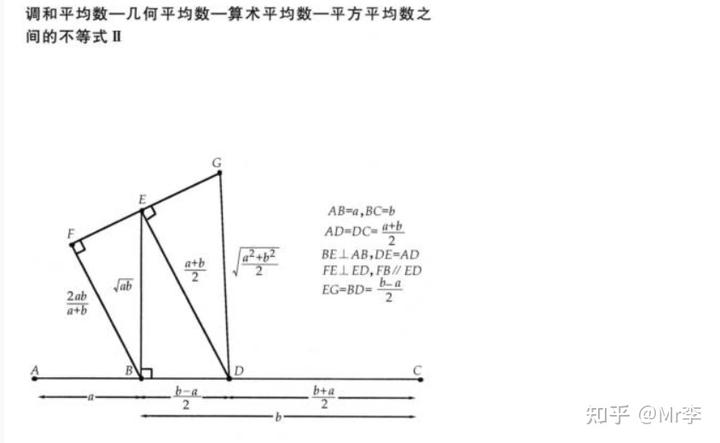
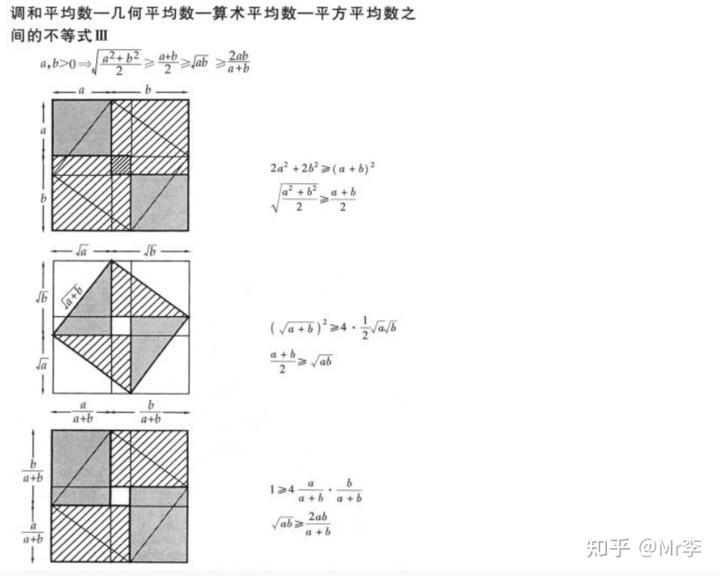
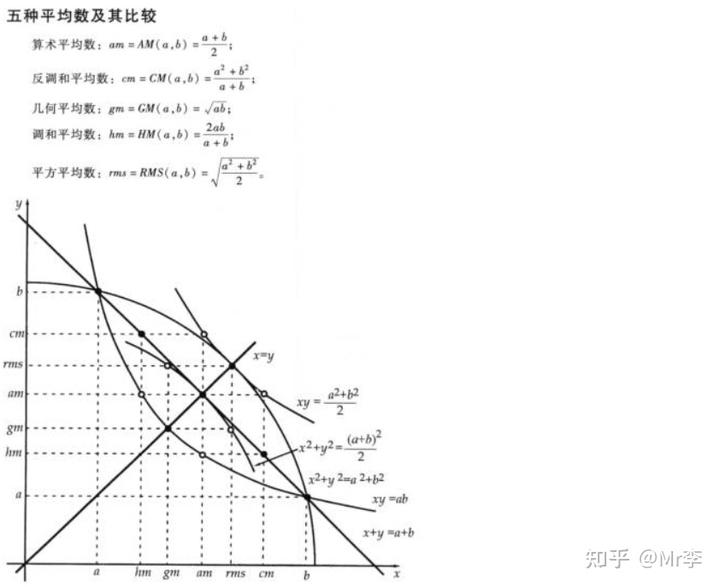
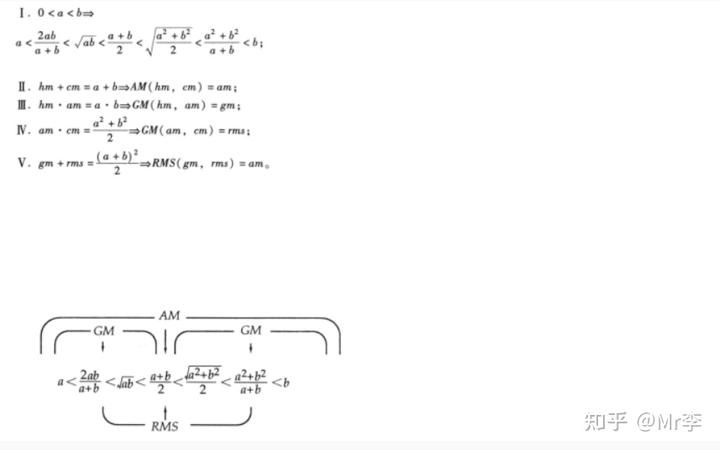
29.算术 - 对数 - 几何平均值不等式
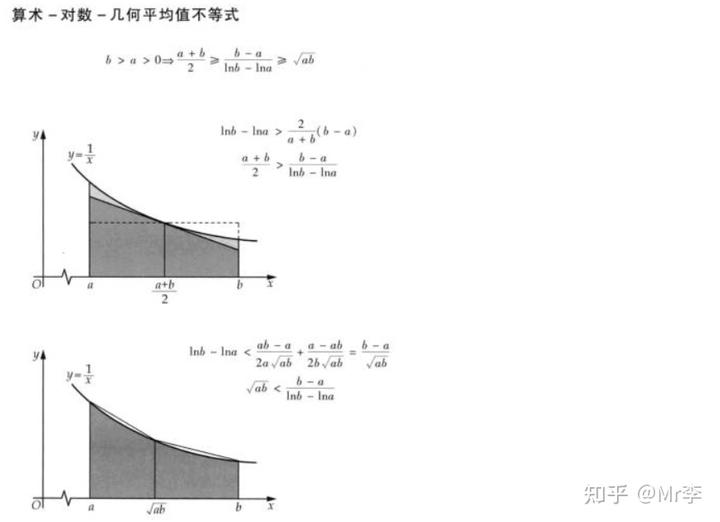
30.单调数列的切比雪夫不等式
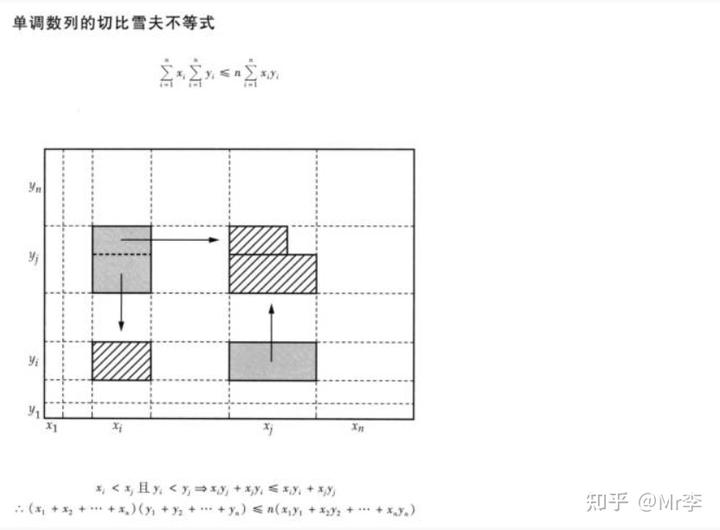
31.用注水实验法验证勾股定理
1. 取直角三角形的三边长 a,b,c ,其中 c 为斜边,分别制作成底面边长为 a,b,c 的正方形,高度相等的长方体容器;
2. 将底面边长为 a,b 的正方体容器注满水,再将两个容器中的水倒入底面边长为 c 的容器中;
3. 奇迹发生了,两个容器中的水恰好可以注满第三个容器!