为何微积分具有如此的优越性?
谢邀。 极限的思想在欧几里得的《几何原本》里就有了,叫做“穷竭法”,一般认为这是欧几里得之前的伟大数学家欧多克索斯发明的。参见我的 《古今数学思想》读书笔记(11) 。 穷竭法的理论基础是《几何原本》第 10 篇的第一个命题:“对于两个不相等的量,若从较大量减去一个比它的一半还要大的量,再从所余量减去大于其半的量,并继续重复执行这一步骤,就能使所余的一个量小于原来那个较小的量。”现在看来,这个命题的实质就是极限定义中的ε—N语言,怪不得是精确的,洞察力令人叹服。柯西和维尔斯特拉斯寻找极限定义时,也许就曾从中吸取智慧。 莫里斯·克莱因在《古今数学思想》里对穷竭法非常推崇:“这方法是严格的,它不含明确的极限步骤。它依赖于间接证法,这样就避免了用极限。实际上欧几里得在面积和体积方面的工作比牛顿和莱布尼茨在这方面的工作严密可靠,因后者试图建立代数方法和数系并且想用极限概念。”刘徽和祖冲之也称得上伟大的数学家了,他们的割圆术也用到了极限的思想,但基本还是一种直觉,严密性远远不如穷竭法。 《几何原本》的第 12、13 篇研究面积和体积,主要方法就是穷竭法。究竟是怎么用的呢?《几何原本》第 12 篇的命题 1 是:“圆内接相似多边形之比等于圆直径平方之比。”很容易证明。命题 2 是关键:“圆与圆之比等于其直径平方之比。” 欧几里得证明的主要精神是,先证明圆可被内接正多边形“穷竭”。从内接正方形开始,它的面积大于圆面积的一半。然后作内接正八边形,可以证明其面积与圆面积的差别小于圆面积与正方形面积之差的一半。如此重复,内接 2^(n+1)边形的面积与圆面积之差总是小于圆面积与内接 2^n 边形面积之差的一半,每一步都把内接多边形与圆的面积差缩小一半以上。根据第十篇命题 1,圆和某一边数足够多的正多边形面积之差可以弄得比任何给定的量还要小。 现设 S 和 S'是两圆面积,d 和 dˊ是其直径。欧几里得要证 S : S' = d^2 : d'^2。假设这等式不成立,而有 S : S˝ = d^2 : d'^2,其中 S˝是大于或小于 S'的某一面积。今设 S˝ < S'。我们在 S'里作边数愈来愈多的正多边形,直到一个 P',使它和 S'的面积差小于 S' - S˝。于是有 S' > P' > S˝。在 S 中作相似于 P'的内接多边形 P。据命题 1,有 P : P' = d^2 : d'^2。但根据前设 S : S˝ = d^2 : d'^2,所以 P : P' = S : S˝,或 P : S = :P' : S˝。但因 P < S,于是 P' < S˝,这与 S' > P' > S˝矛盾。同样可证 S˝ > S'也不能成立,因此 S˝ = S',证毕。 然后欧几里得用穷竭法证明下面这些重要而难证的定理: “命题 5、底为三角形而高相等的棱锥之比等于其底之比。” “命题 10、任一[正]圆锥是与其同底等高圆柱的三分之一。” “命题 11、同高的圆锥[与圆锥]以及同高的圆柱[与圆柱]之比等于其底之比。” “命题 12、相似的圆锥之间以及圆柱之间的比,等于其底直径的三次比[立方之比]。” “命题 18、球之比等于其直径的三次比。” 后来阿基米德把穷竭法用得更加出神入化,解出了抛物线弓形的面积、螺线第一圈与初始线所围的面积等困难的问题。参见我的 《古今数学思想》读书笔记(15) 。这些更是中国古代数学家们想象不到的了,因为中国古代研究过的曲线基本只有圆,完全没考虑过圆锥曲线、螺线。 但是穷竭法到阿基米德这里就看出问题来了。求螺线下面积时,他选取的是越来越小的扇形,而不是用越来越多的直边形来穷竭。可见穷竭法是一种非常需要技巧的方法,阿基米德的神奇之处就在于针对每个问题设计巧妙的穷竭途径。那么遇到更复杂的问题怎么办? 微积分的强大,就在于把这些令人绞尽脑汁的技巧抹平了。你一下子获得了通用的办法,因为你发现,真正重要的是穷竭的思想,而穷竭的途径呢,随便用什么图形都可以,结果都一样。从此以后,天才的设计让位于傻瓜的算法,人们可以节约大量的脑力、时间来处理更深入的问题了。 这给我们的启示是,如果你发现有一类问题可以解,但需要非常繁琐的技巧,那么很可能你已经触及了这类问题的本质,但尚未明确地理解本质。一旦你把本质提炼出来,结果就是思维和工具的极大简化。 正如希尔伯特所说:“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着,这些工具和方法同时会有助于已有的理论并把陈旧的、复杂的东西抛到一边。数学科学发展的这种特点是根深蒂固的。” 查看知乎讨论


谢邀。
极限的思想在欧几里得的《几何原本》里就有了,叫做“穷竭法”,一般认为这是欧几里得之前的伟大数学家欧多克索斯发明的。参见我的
。
穷竭法的理论基础是《几何原本》第 10 篇的第一个命题:“对于两个不相等的量,若从较大量减去一个比它的一半还要大的量,再从所余量减去大于其半的量,并继续重复执行这一步骤,就能使所余的一个量小于原来那个较小的量。”现在看来,这个命题的实质就是极限定义中的ε—N语言,怪不得是精确的,洞察力令人叹服。柯西和维尔斯特拉斯寻找极限定义时,也许就曾从中吸取智慧。
莫里斯·克莱因在《古今数学思想》里对穷竭法非常推崇:“这方法是严格的,它不含明确的极限步骤。它依赖于间接证法,这样就避免了用极限。实际上欧几里得在面积和体积方面的工作比牛顿和莱布尼茨在这方面的工作严密可靠,因后者试图建立代数方法和数系并且想用极限概念。”刘徽和祖冲之也称得上伟大的数学家了,他们的割圆术也用到了极限的思想,但基本还是一种直觉,严密性远远不如穷竭法。
《几何原本》的第 12、13 篇研究面积和体积,主要方法就是穷竭法。究竟是怎么用的呢?《几何原本》第 12 篇的命题 1 是:“圆内接相似多边形之比等于圆直径平方之比。”很容易证明。命题 2 是关键:“圆与圆之比等于其直径平方之比。”
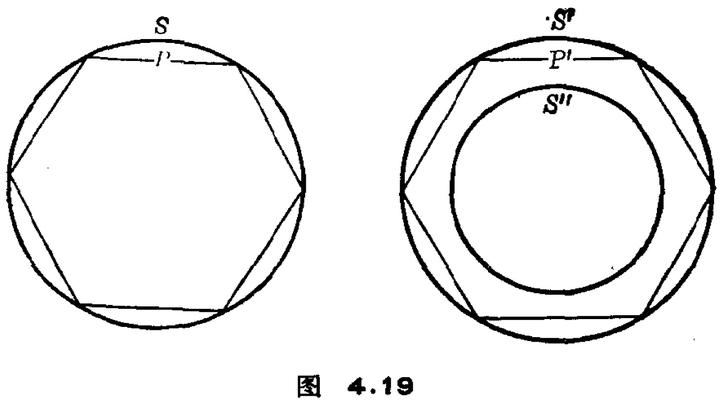
欧几里得证明的主要精神是,先证明圆可被内接正多边形“穷竭”。从内接正方形开始,它的面积大于圆面积的一半。然后作内接正八边形,可以证明其面积与圆面积的差别小于圆面积与正方形面积之差的一半。如此重复,内接 2^(n+1)边形的面积与圆面积之差总是小于圆面积与内接 2^n 边形面积之差的一半,每一步都把内接多边形与圆的面积差缩小一半以上。根据第十篇命题 1,圆和某一边数足够多的正多边形面积之差可以弄得比任何给定的量还要小。
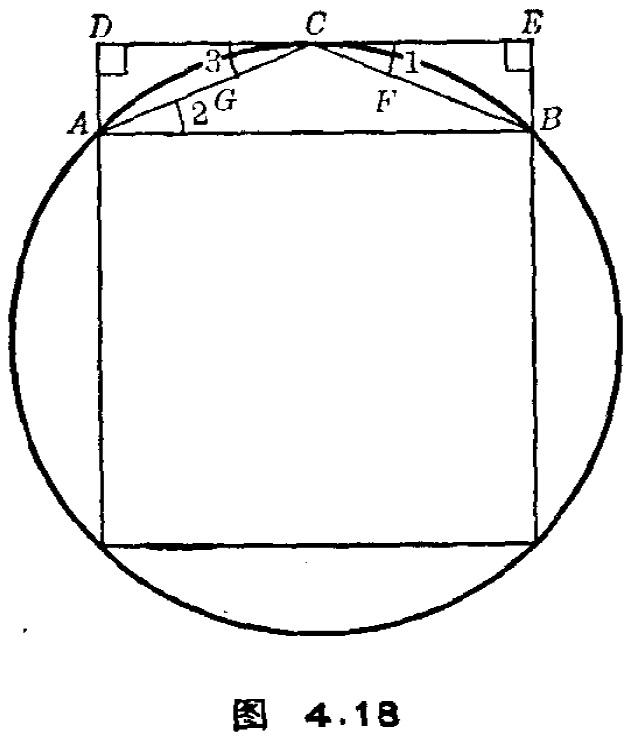
现设 S 和 S'是两圆面积,d 和 dˊ是其直径。欧几里得要证 S : S' = d^2 : d'^2。假设这等式不成立,而有 S : S˝ = d^2 : d'^2,其中 S˝是大于或小于 S'的某一面积。今设 S˝ < S'。我们在 S'里作边数愈来愈多的正多边形,直到一个 P',使它和 S'的面积差小于 S' - S˝。于是有 S' > P' > S˝。在 S 中作相似于 P'的内接多边形 P。据命题 1,有 P : P' = d^2 : d'^2。但根据前设 S : S˝ = d^2 : d'^2,所以 P : P' = S : S˝,或 P : S = :P' : S˝。但因 P < S,于是 P' < S˝,这与 S' > P' > S˝矛盾。同样可证 S˝ > S'也不能成立,因此 S˝ = S',证毕。
然后欧几里得用穷竭法证明下面这些重要而难证的定理:
“命题 5、底为三角形而高相等的棱锥之比等于其底之比。”
“命题 10、任一[正]圆锥是与其同底等高圆柱的三分之一。”
“命题 11、同高的圆锥[与圆锥]以及同高的圆柱[与圆柱]之比等于其底之比。”
“命题 12、相似的圆锥之间以及圆柱之间的比,等于其底直径的三次比[立方之比]。”
“命题 18、球之比等于其直径的三次比。”
后来阿基米德把穷竭法用得更加出神入化,解出了抛物线弓形的面积、螺线第一圈与初始线所围的面积等困难的问题。参见我的
。这些更是中国古代数学家们想象不到的了,因为中国古代研究过的曲线基本只有圆,完全没考虑过圆锥曲线、螺线。
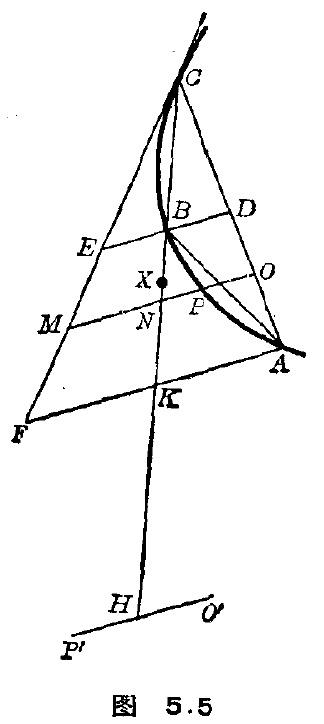
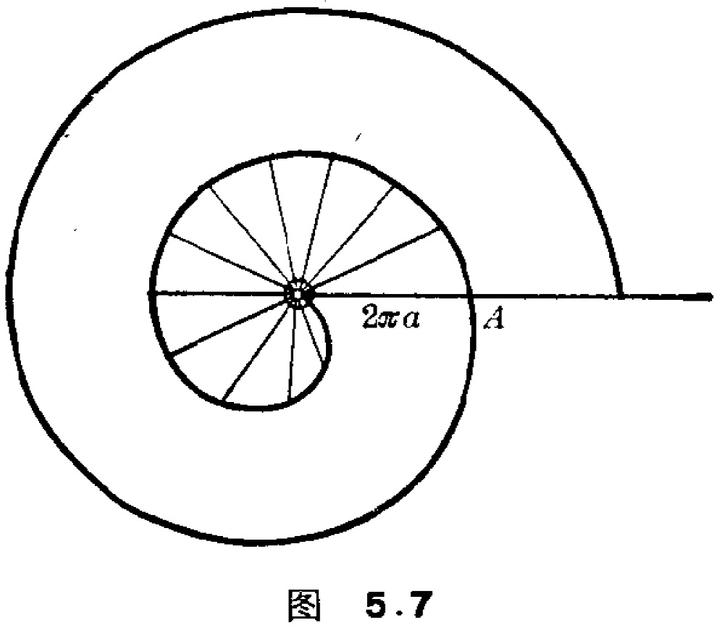
但是穷竭法到阿基米德这里就看出问题来了。求螺线下面积时,他选取的是越来越小的扇形,而不是用越来越多的直边形来穷竭。可见穷竭法是一种非常需要技巧的方法,阿基米德的神奇之处就在于针对每个问题设计巧妙的穷竭途径。那么遇到更复杂的问题怎么办?
微积分的强大,就在于把这些令人绞尽脑汁的技巧抹平了。你一下子获得了通用的办法,因为你发现,真正重要的是穷竭的思想,而穷竭的途径呢,随便用什么图形都可以,结果都一样。从此以后,天才的设计让位于傻瓜的算法,人们可以节约大量的脑力、时间来处理更深入的问题了。
这给我们的启示是,如果你发现有一类问题可以解,但需要非常繁琐的技巧,那么很可能你已经触及了这类问题的本质,但尚未明确地理解本质。一旦你把本质提炼出来,结果就是思维和工具的极大简化。
正如希尔伯特所说:“数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着,这些工具和方法同时会有助于已有的理论并把陈旧的、复杂的东西抛到一边。数学科学发展的这种特点是根深蒂固的。”