如何通俗易懂地解释「协方差」与「相关系数」的概念?
最喜欢通俗易懂地解释一个事情。 一、协方差: 可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何? 你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的。 你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的。 从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。 咱们从公式出发来理解一下: 公式简单翻译一下是:如果有 X,Y 两个变量,每个时刻的“X 值与其均值之差”乘以“Y 值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值(其实是求“期望”,但就不引申太多新概念了,简单认为就是求均值了)。 下面举个例子来说明吧: 比如有两个变量 X,Y,观察 t1-t7(7 个时刻)他们的变化情况。 简单做了个图:分别用红点和绿点表示 X、Y,横轴是时间。可以看到 X,Y 均围绕各自的均值运动,并且很明显是同向变化的。 这时,我们发现每一时刻 的值与 的值的“正负号”一定相同(如下图:比如 t1 时刻,他们同为正,t2 时刻他们同为负): 所以,像上图那样,当他们同向变化时, 与 的乘积为正。这样,当你把 t1-t7 时刻 与 的乘积加在一起,求平均后也就是正数了。 如果反向运动呢? 很明显, 的值与 的值的“正负号”一定相反,于是 与 的乘积就是负值了。这样当你把 t1-t7 时刻 与 的乘积加在一起,求平均的时候也就是负数了。 当然上面说的是两种特殊情况,很多时候 X,Y 的运动是不规律的,比如: 这时,很可能某一时刻 的值与 的值乘积为正,另外一个时刻 的值与 的值乘积为负。 将每一时刻 与 的乘积加在一起,其中的正负项就会抵消掉,最后求平均得出的值就是协方差,通过协方差的数值大小,就可以判断这两个变量同向或反向的程度了。 所以,t1-t7 时刻中, 与 的乘积为正的越多,说明同向变化的次数越多,也即同向程度越高。反之亦然。 总结一下,如果协方差为正,说明 X,Y 同向变化,协方差越大说明同向程度越高;如果协方差为负,说明 X,Y 反向运动,协方差越小说明反向程度越高。 --------LINE--------- 一般的同学看到 above the line 的内容就 ok 了。但有一些爱钻研的同学,可能会进一步提问: 那如果 X,Y 同向变化,但 X 大于均值,Y 小于均值,那 与 的乘积为负值啊?这不是矛盾了吗? 那就继续往下看…… 这种情况是有可能出现的,比如: 可以看到,t1 时刻, 与 的符号相反,他们的乘积为负值。 但是,总体看,这两个变量的协方差仍然是正的,因为你还要计算 t2,t3……t7 时刻 与 的乘积,然后再把这 7 个时刻的乘积求和做均值,才是最后 X,Y 的协方差。1 个负、6 个正,显然最后协方差很大可能性是正的。 所以 t1 时刻 与 的乘积为负值,并不能说明他们反向运动,要结合整体的情况来判断。 那么你可能又要问了,既然都是同向变化,那 t1 时刻 与 的乘积为负值、其他时刻乘积为正的这种情况,与,t1-t7 时刻 与 的乘积均为正值的情况,到底有什么差异呢?这点其实前面也解释过了,差异就是:第一种情况的同向程度不如第二种情况的同向程度大(第一种情况 6 正 1 负,第二种情况 7 正,所以第一种情况的协方差小于第二种情况的协方差,第一种情况 X,Y 变化的同向程度要小于第二种情况)。 另外,如果你还钻牛角尖,说如果 t1,t2,t3……t7 时刻 X,Y 都在增大,而且 X 都比均值大,Y 都比均值小,这种情况协方差不就是负的了?7 个负值求平均肯定是负值啊?但是 X,Y 都是增大的,都是同向变化的,这不就矛盾了? 这个更好解释了:这种情况不可能出现! 因为,你的均值算错了…… X,Y 的值应该均匀的分布在均值两侧才对,不可能都比均值大,或都比均值小。 所以,实际它的图应该是下面这样的: 发现没有,又变成 与 的符号相同的情况了~有没有种被大自然打败的感觉~ 好了,现在,对于协方差应该有点感觉了吧? 二、相关系数: 对于相关系数,我们从它的公式入手。一般情况下,相关系数的公式为: 翻译一下:就是用 X、Y 的协方差除以 X 的标准差和 Y 的标准差。 所以,相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。 既然是一种特殊的协方差,那它: 1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。 2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。 比较抽象,下面还是举个例子来说明: 首先,还是承接上文中的变量 X、Y 变化的示意图(X 为红点,Y 为绿点),来看两种情况: 很容易就可以看出以上两种情况 X,Y 都是同向变化的,而这个“同向变化”,有个非常显著特征:X、Y 同向变化的过程,具有极高的相似度!无论第一还是第二种情况下,都是:t1 时刻 X、Y 都大于均值,t2 时刻 X、Y 都变小且小于均值,t3 时刻 X、Y 继续变小且小于均值,t4 时刻 X、Y 变大但仍小于均值,t5 时刻 X、Y 变大且大于均值…… 可是,计算一下他们的协方差, 第一种情况下: 第二种情况下: 协方差差出了一万倍,只能从两个协方差都是正数判断出两种情况下 X、Y 都是同向变化,但是,一点也看不出两种情况下 X、Y 的变化都具有相似性这一特点。 这是为什么呢? 因为以上两种情况下,在 X、Y 两个变量同向变化时,X 变化的幅度不同,这样,两种情况的协方差更多的被变量的变化幅度所影响了。 所以,为了能准确的研究两个变量在变化过程中的相似程度,我们就要把变化幅度对协方差的影响,从协方差中剔除掉。于是,相关系数就横空出世了,就有了最开始相关系数的公式: 那么为什么要通过除以标准差的方式来剔除变化幅度的影响呢?咱们简单从标准差公式看一下: 从公式可以看出,标准差计算方法为,每一时刻变量值与变量均值之差再平方,求得一个数值,再将每一时刻这个数值相加后求平均,再开方。 “变量值与变量均值之差” 是什么呢?就是偏离均值的幅度: 那为何要对它做平方呢?因为有时候变量值与均值是反向偏离的(见下图), 是个负数,平方后,就可以把负号消除了。这样在后面求平均时,每一项数值才不会被正负抵消掉,最后求出的平均值才能更好的体现出每次变化偏离均值的情况。 当然,最后求出平均值后并没有结束,因为刚才为了消除负号,把 进行了平方,那最后肯定要把求出的均值开方,将这个偏离均值的幅度还原回原来的量级。于是就有了下面标准差的公式: 所以标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差,也就是把协方差中变量变化幅度对协方差的影响剔除掉,这样协方差也就标准化了,它反应的就是两个变量每单位变化时的情况。这也就是相关系数的公式含义了。 同时,你可以反过来想象一下:既然相关系数是协方差除以标准差,那么,当 X 或 Y 的波动幅度变大的时候,它们的协方差会变大,标准差也会变大,这样相关系数的分子分母都变大,其实变大的趋势会被抵消掉,变小时也亦然。于是,很明显的,相关系数不像协方差一样可以在+ 到- 间变化,它只能在+1 到-1 之间变化(相关系数的取值范围在+1 到-1 之间变化可以通过施瓦茨不等式来证明,有些复杂,这里就不赘述了,有兴趣的可以 google 下)。 总结一下,对于两个变量 X、Y, 当他们的相关系数为 1 时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以 X、Y 为横纵坐标轴,可以画出一条斜率为正数的直线,所以 X、Y 是线性关系的)。 随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为 0 时,两个变量的变化过程没有任何相似度,也即两个变量无关。 当相关系数继续变小,小于 0 时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。 当相关系数为-1 时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以 X、Y 为横纵坐标轴,可以画出一条斜率为负数的直线,所以 X、Y 也是线性关系的)。 有了上面的背景,我们再回到最初的变量 X、Y 的例子中,可以先看一下第一种情况的相关系数: X 的标准差为 Y 的标准差为 于是相关系数为 说明第一种情况下,X 的变化与 Y 的变化具有很高的相似度,而且已经接近完全正相关了,X、Y 几乎就是线性变化的。 那第二种情况呢? X 的标准差为 Y 的标准差为 于是相关系数为 说明第二种情况下,虽然 X 的变化幅度比第一种情况 X 的变化幅度小了 10000 倍,但是丝毫没有改变“X 的变化与 Y 的变化具有很高的相似度”这一结论。同时,由于第一种、第二种情况的相关系数是相等的,因此在这两种情况下,X、Y 的变化过程有着同样的相似度。 好了,讲了这么多,不知你看完是否对相关系数也有了一些感觉? 三、写在最后 本文主要还是想给非理工专业、入门级的各位朋友看的,自己也曾在茫茫公式海中痛苦过,但后来发现对一个公式的原理有了一个感觉后,它也就变得好记很多了,而且也愿意深入研究它了。这篇文章也就是培养你对于协方差、相关系数的这种感觉。但是,为了通俗易懂,有些地方也不够全面、严谨。也许你看完本文,经过自己的学习研究,也会有自己的一些想法,那你可以继续研究一下本题目下其他答主的答案,通过引入向量、内积等定义,会把协方差、相关系数说明得更加严谨和透彻。总之学习是一个循序渐进的过程,不要觉得彻底明白了什么,那往往是你踏入一个领域的第一步。 (完) 其他一些推荐的通俗易懂类答案,感兴趣的朋友可以阅读: 作为一个非金融从业者怎样才能看懂电影《大空头》? - GRAYLAMB 的回答 - 知乎 关于外汇标价方法的定义,直接标价法到底是什么? - GRAYLAMB 的回答 - 知乎 如何浅显易懂地解说 Paxos 的算法? 未来计划继续通俗易懂解读 ApplePay、区块链、机器学习,欢迎关注。 ——2017.2.25 关于比特币与区块链的文章写好了,有兴趣的可以来瞅瞅~ GRAYLAMB:比特币 (Bitcoin) 系统是如何运行的? ——2017.8.4 查看知乎讨论

最喜欢通俗易懂地解释一个事情。
一、协方差:
可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?
你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的。
你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的。
从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
咱们从公式出发来理解一下:
公式简单翻译一下是:如果有 X,Y 两个变量,每个时刻的“X 值与其均值之差”乘以“Y 值与其均值之差”得到一个乘积,再对这每时刻的乘积求和并求出均值(其实是求“期望”,但就不引申太多新概念了,简单认为就是求均值了)。
下面举个例子来说明吧:
比如有两个变量 X,Y,观察 t1-t7(7 个时刻)他们的变化情况。
简单做了个图:分别用红点和绿点表示 X、Y,横轴是时间。可以看到 X,Y 均围绕各自的均值运动,并且很明显是同向变化的。
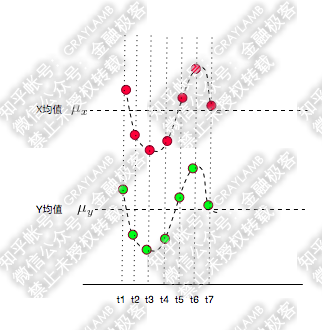
这时,我们发现每一时刻
的值与
的值的“正负号”一定相同(如下图:比如 t1 时刻,他们同为正,t2 时刻他们同为负):
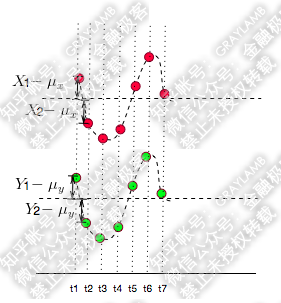
所以,像上图那样,当他们同向变化时,
与
的乘积为正。这样,当你把 t1-t7 时刻
与
的乘积加在一起,求平均后也就是正数了。
如果反向运动呢?
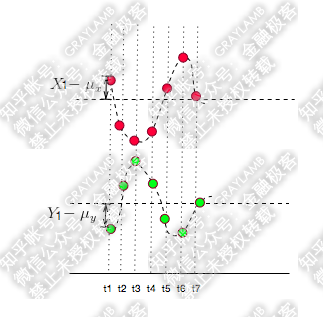
很明显,
的值与
的值的“正负号”一定相反,于是
与
的乘积就是负值了。这样当你把 t1-t7 时刻
与
的乘积加在一起,求平均的时候也就是负数了。
当然上面说的是两种特殊情况,很多时候 X,Y 的运动是不规律的,比如:
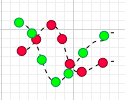
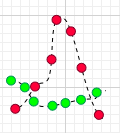
这时,很可能某一时刻
的值与
的值乘积为正,另外一个时刻
的值与
的值乘积为负。
将每一时刻
与
的乘积加在一起,其中的正负项就会抵消掉,最后求平均得出的值就是协方差,通过协方差的数值大小,就可以判断这两个变量同向或反向的程度了。
所以,t1-t7 时刻中,
与
的乘积为正的越多,说明同向变化的次数越多,也即同向程度越高。反之亦然。
总结一下,如果协方差为正,说明 X,Y 同向变化,协方差越大说明同向程度越高;如果协方差为负,说明 X,Y 反向运动,协方差越小说明反向程度越高。
--------LINE---------
一般的同学看到 above the line 的内容就 ok 了。但有一些爱钻研的同学,可能会进一步提问:
那如果 X,Y 同向变化,但 X 大于均值,Y 小于均值,那
与
的乘积为负值啊?这不是矛盾了吗?
那就继续往下看……
这种情况是有可能出现的,比如:
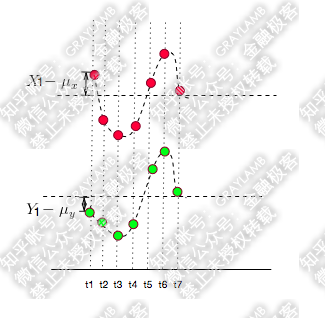
可以看到,t1 时刻,
与
的符号相反,他们的乘积为负值。
但是,总体看,这两个变量的协方差仍然是正的,因为你还要计算 t2,t3……t7 时刻
与
的乘积,然后再把这 7 个时刻的乘积求和做均值,才是最后 X,Y 的协方差。1 个负、6 个正,显然最后协方差很大可能性是正的。
所以 t1 时刻
与
的乘积为负值,并不能说明他们反向运动,要结合整体的情况来判断。
那么你可能又要问了,既然都是同向变化,那 t1 时刻
与
的乘积为负值、其他时刻乘积为正的这种情况,与,t1-t7 时刻
与
的乘积均为正值的情况,到底有什么差异呢?这点其实前面也解释过了,差异就是:第一种情况的同向程度不如第二种情况的同向程度大(第一种情况 6 正 1 负,第二种情况 7 正,所以第一种情况的协方差小于第二种情况的协方差,第一种情况 X,Y 变化的同向程度要小于第二种情况)。
另外,如果你还钻牛角尖,说如果 t1,t2,t3……t7 时刻 X,Y 都在增大,而且 X 都比均值大,Y 都比均值小,这种情况协方差不就是负的了?7 个负值求平均肯定是负值啊?但是 X,Y 都是增大的,都是同向变化的,这不就矛盾了?
这个更好解释了:这种情况不可能出现!
因为,你的均值算错了……
X,Y 的值应该均匀的分布在均值两侧才对,不可能都比均值大,或都比均值小。
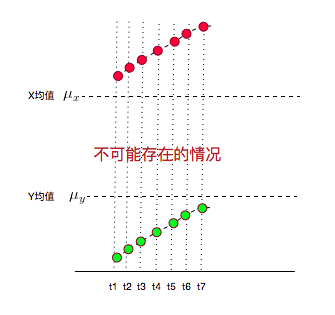
所以,实际它的图应该是下面这样的:
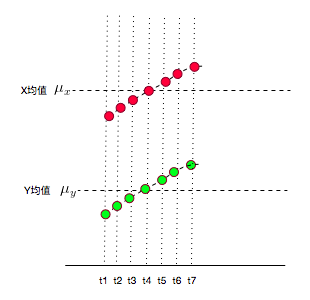
发现没有,又变成
与
的符号相同的情况了~有没有种被大自然打败的感觉~
好了,现在,对于协方差应该有点感觉了吧?
二、相关系数:
对于相关系数,我们从它的公式入手。一般情况下,相关系数的公式为:
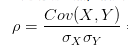
翻译一下:就是用 X、Y 的协方差除以 X 的标准差和 Y 的标准差。
所以,相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
比较抽象,下面还是举个例子来说明:
首先,还是承接上文中的变量 X、Y 变化的示意图(X 为红点,Y 为绿点),来看两种情况:
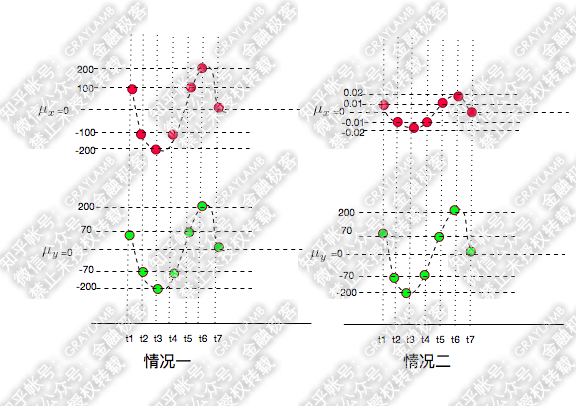
很容易就可以看出以上两种情况 X,Y 都是同向变化的,而这个“同向变化”,有个非常显著特征:X、Y 同向变化的过程,具有极高的相似度!无论第一还是第二种情况下,都是:t1 时刻 X、Y 都大于均值,t2 时刻 X、Y 都变小且小于均值,t3 时刻 X、Y 继续变小且小于均值,t4 时刻 X、Y 变大但仍小于均值,t5 时刻 X、Y 变大且大于均值……
可是,计算一下他们的协方差,
第一种情况下:
第二种情况下:
协方差差出了一万倍,只能从两个协方差都是正数判断出两种情况下 X、Y 都是同向变化,但是,一点也看不出两种情况下 X、Y 的变化都具有相似性这一特点。
这是为什么呢?
因为以上两种情况下,在 X、Y 两个变量同向变化时,X 变化的幅度不同,这样,两种情况的协方差更多的被变量的变化幅度所影响了。
所以,为了能准确的研究两个变量在变化过程中的相似程度,我们就要把变化幅度对协方差的影响,从协方差中剔除掉。于是,相关系数就横空出世了,就有了最开始相关系数的公式:
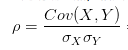
那么为什么要通过除以标准差的方式来剔除变化幅度的影响呢?咱们简单从标准差公式看一下:
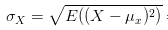
从公式可以看出,标准差计算方法为,每一时刻变量值与变量均值之差再平方,求得一个数值,再将每一时刻这个数值相加后求平均,再开方。
“变量值与变量均值之差”
是什么呢?就是偏离均值的幅度:
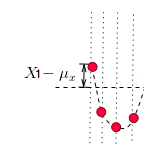
那为何要对它做平方呢?因为有时候变量值与均值是反向偏离的(见下图),
是个负数,平方后,就可以把负号消除了。这样在后面求平均时,每一项数值才不会被正负抵消掉,最后求出的平均值才能更好的体现出每次变化偏离均值的情况。
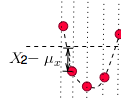
当然,最后求出平均值后并没有结束,因为刚才为了消除负号,把
进行了平方,那最后肯定要把求出的均值开方,将这个偏离均值的幅度还原回原来的量级。于是就有了下面标准差的公式:
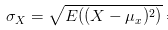
所以标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差,也就是把协方差中变量变化幅度对协方差的影响剔除掉,这样协方差也就标准化了,它反应的就是两个变量每单位变化时的情况。这也就是相关系数的公式含义了。
同时,你可以反过来想象一下:既然相关系数是协方差除以标准差,那么,当 X 或 Y 的波动幅度变大的时候,它们的协方差会变大,标准差也会变大,这样相关系数的分子分母都变大,其实变大的趋势会被抵消掉,变小时也亦然。于是,很明显的,相关系数不像协方差一样可以在+
到-
间变化,它只能在+1 到-1 之间变化(相关系数的取值范围在+1 到-1 之间变化可以通过施瓦茨不等式来证明,有些复杂,这里就不赘述了,有兴趣的可以 google 下)。
总结一下,对于两个变量 X、Y,
当他们的相关系数为 1 时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以 X、Y 为横纵坐标轴,可以画出一条斜率为正数的直线,所以 X、Y 是线性关系的)。
随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为 0 时,两个变量的变化过程没有任何相似度,也即两个变量无关。
当相关系数继续变小,小于 0 时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。
当相关系数为-1 时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以 X、Y 为横纵坐标轴,可以画出一条斜率为负数的直线,所以 X、Y 也是线性关系的)。
有了上面的背景,我们再回到最初的变量 X、Y 的例子中,可以先看一下第一种情况的相关系数:
X 的标准差为
Y 的标准差为
于是相关系数为
说明第一种情况下,X 的变化与 Y 的变化具有很高的相似度,而且已经接近完全正相关了,X、Y 几乎就是线性变化的。
那第二种情况呢?
X 的标准差为
Y 的标准差为
于是相关系数为
说明第二种情况下,虽然 X 的变化幅度比第一种情况 X 的变化幅度小了 10000 倍,但是丝毫没有改变“X 的变化与 Y 的变化具有很高的相似度”这一结论。同时,由于第一种、第二种情况的相关系数是相等的,因此在这两种情况下,X、Y 的变化过程有着同样的相似度。
好了,讲了这么多,不知你看完是否对相关系数也有了一些感觉?
三、写在最后
本文主要还是想给非理工专业、入门级的各位朋友看的,自己也曾在茫茫公式海中痛苦过,但后来发现对一个公式的原理有了一个感觉后,它也就变得好记很多了,而且也愿意深入研究它了。这篇文章也就是培养你对于协方差、相关系数的这种感觉。但是,为了通俗易懂,有些地方也不够全面、严谨。也许你看完本文,经过自己的学习研究,也会有自己的一些想法,那你可以继续研究一下本题目下其他答主的答案,通过引入向量、内积等定义,会把协方差、相关系数说明得更加严谨和透彻。总之学习是一个循序渐进的过程,不要觉得彻底明白了什么,那往往是你踏入一个领域的第一步。
(完)
其他一些推荐的通俗易懂类答案,感兴趣的朋友可以阅读:
作为一个非金融从业者怎样才能看懂电影《大空头》? - GRAYLAMB 的回答 - 知乎
关于外汇标价方法的定义,直接标价法到底是什么? - GRAYLAMB 的回答 - 知乎
未来计划继续通俗易懂解读 ApplePay、区块链、机器学习,欢迎关注。
——2017.2.25
关于比特币与区块链的文章写好了,有兴趣的可以来瞅瞅~
GRAYLAMB:比特币 (Bitcoin) 系统是如何运行的?
——2017.8.4